ここでは油圧や昇降機構について行った理論計算について掲載します。私には高校の授業程度の計算しかできませんのでその程度です。また、この計算の考え方が全て本当に正しいかどうかはわかりません。あくまでも私なりに行った計算です。(5の➁以降)
製作後に計算したものもあります。
なお、鉄骨材料の強度計算については全く知識が無かったので最初からやる考えが無く、製作に当たっては感を頼りに材料を決めていくというやり方で進めてしまいます。
5.昇降機構と油圧の理論的な検討
「理論的な検討」などというタイトルで、大変おこがましいのですがはじめます。
計算の元になる値は「高所作業車自作 その1 主要材料調達」に記載したものを使いました。
数値の標記はエクセルなどで使われている指数形式も使っています。
例1 12000000 = 12×10^6 = 12E6
例2 0.0025 = 2.5×10^-3 = 2.5E-3
➀ 油圧シリンダの最大推力
シリンダは押し方向で使います。
シリンダの内径 r = シリンダ外径φ60-13 = φ47[mm]= 0.047[m](想定値) シリンダ内径の断面積 A = π・r^2 = 3.14159×(φ0.047/2)^2 = 0.001735[㎡] 油圧ポンプの最高圧力 P = 12[MPa]= 12000000[Pa]= 12E6[Pa] シリンダ推力 F = A・P = 1.735E-3 x 12E6 = 20820[N]= 2124[kgf]= 2.124[tf]
上記の検討は、スタクセル・エンジニアリング様にして頂いたものを私なりにまとめ直したものです。
➁ 必要油量
このシリンダを最大に伸ばすための必要油量を求めてみます。
ストローク L = 300[mm]= 0.3[m] 必要油量 Q = A・L = 0.001735 × 0.3 = 0.00052[㎥]= 0.52[l](リットル) ★ タンク油量が2[l]なので問題なし。
➂ 油圧シリンダの伸長速度
油圧ポンプ吐出量 b = 2.1[ml/r]= 2.1E-6[㎥/r] 油圧ポンプ回転数 n = 2500[rpm]= 2500/60[rps] = 41.7[rps](目安値より) 油圧吐出量 q = b・n = 2.1E-6 × 41.7 = 88E-6[㎥/s] シリンダ伸長速度 v = q/A = 88E-6/1.735E-3 ≒ 0.05[m/s]= 5[cm/s]
➃ リンク式昇降機構の必要推力
昇降機構のリンクの各部にはどんな力が掛かるのか計算してみたいと思い、いろいろと考えてみましたが簡単にはできそうもありませんでした。そこでできるだけ単純化して考え、最悪の状態を概算してみることにしました。
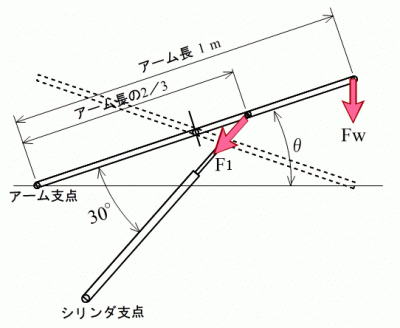
図1のように、まず1段目のリンクだけで考えアームの長さを1mとします。
クロスしたアームの内一方(実線の方)だけに負荷重力が掛かると考えます。この時、アームの左端が支点、2/3の所が力点、右端が作用点になります。負荷総重力Fwが作用点に掛かります。
シリンダとアームとの成す角は実際には変化しますが、それ程大きな変化は無いと考えて30°固定とします。
シリンダが伸びアームが上昇するにつれて角θが次第に大きくなります。シリンダに加わる力F1は、θ=0の時が最も大きいのでその状態で計算していくことにします。
なお、アームは左右に計2本ありますが、ここでは2本分を1本としてまとめて計算していきます。従って、左右均等に力が掛かるとすれば、実際に1本当たりに掛かる力はこの計算値の1/2となります。
負荷重力の仮定 昇降機構の重力=100kgf、乗る人の重力=60kgf、載せる荷物の重力=40kgf 負荷総重力 Fw = 100+60+40 = 200[kgf](= 200×9.8[N]= 1960[N]) シリンダに掛かる力 F1 = Fw・3/2/sin30° = 200×3/2/0.5 = 600[kgf]= 0.6[tf](= 5880[N]) リンクの段数が2段ならシリンダに掛かる力も2倍となり 1.2[tf] リンクの段数が3段ならシリンダに掛かる力も3倍となり 1.8[tf] ★ 何れも油圧シリンダの最大推力2.124[tf]を下回るため上昇可能。 なお、力点がより右に移動するほどシリンダに掛かる力が減り、余裕も大きくなる。
⑤ 昇降機構の上昇速度
前項と同条件で計算しました。θ=0の時、上昇速度が最も速いと思われます。
シリンダの伸長速度 v = 0.05[m/s] リンク1段当たりの速度 v1 = v・3/2/sin30° = 0.05×3/2/0.5 = 0.15[m/s] リンクが2段なら速度も2倍となり 0.30[m/s] リンクが3段なら速度も3倍となり 0.45[m/s] 力点がより右に移動するほど速度は遅くなる。 ★ 少々速過ぎるのではないか?。
この段階ではどうしようもないので、まずは製作し動かして様子を見ることにしました。
⑥ アームに掛かる曲げモーメント
実線で書いた側のアームにはシリンダが接続されている力点に曲げモーメントが掛かります。また、反対側の点線で書いた側のアームには軸である中央部に曲げモーメントが掛かります。いままでと同条件で計算してみました。
実線側のアームの曲げモーメント Ma = 力×腕の長さ = 1960[N]×1/3[m] = 653[N・m] 点線側のアームの曲げモーメント Mb = 力×腕の長さ = 1960[N]×1/2[m] = 830[N・m] (下の計算は点線側のアームに全ての負荷総重力が掛かったと考えた場合) 実際には、これにリンクの段数を掛けたものとなる。
機構が静止している状態でシリンダの推力が加わったときには、推力そのものが曲げモーメントとして衝撃的に掛かるのではないかと思われます。その値を計算してみると
点線側のアームで求めると 上昇開始時 Mb'= 20820[N]×1/2[m] = 10410[N・m] これは、上で計算した静的なモーメントをはるかに超える値である。
実は試乗中に最下部のアームが見事に折れ曲がるという事故に遭いました(幸い私は無事でしたが)。上の図1で示す点線側のアームが中央部で見事に破断しました。また、実線側のアームもシリンダー接続部で少し湾曲していました。アーム材の強度が不足していたためです。
また、最下部から上昇をはじめた途端に事故が起きましたので、まさしく衝撃的に大きな曲げモーメントが掛かったと想像できます。
アームに掛かる力が結構複雑だったため別のことが頭を占め、この曲げモーメントのことがすっかり落ちていました。破損して改めて思い知らされました。どのみち私の力では材料の強度計算まではできませんが、この部分の破断を予想することもできなかったのが悔しい気持ちです。
⑦ アームに掛かる力の検討
アーム各部への力の掛かり方は一部は予想できたのですが、総合的にまとめることができず製作が先に進行しました。今このブログをまとめる中で段々と整理されてきて総合的に検討できるようになってきました。その検討の結果を、理論計算2 として新たに起こして掲載しましたのでそちらをご覧下さい。
関連ページ
高所作業車自作 概要
高所作業車自作 その1 主要材料調達
高所作業車自作 その2 理論計算1
高所作業車自作 その3 製作
高所作業車自作 その4 仮組立とアーム破断
高所作業車自作 その5 塗装と最終組立
高所作業車自作 その6 理論計算2
高所作業車自作 その7 強度計算にチャレンジ