ここへ来てやっと、各部に掛かる力の解明が自分なりに納得できる形でできました。あくまで私の考え方で行ったものですので保証はありませんが、何回も検算をして確かめてきた結果です。根本的な考え方の誤り、細かい誤り等ありましたらご指摘いただけると嬉しいです。
17.各部に掛かる力
力の掛かり方と計算結果
今回行った計算の全てを次に掲載します。
➀ 数式による理論的な解明 pdf
➁ θを変化させて計算した結果 エクセル(xlsx) pdfに変換したもの
エクセルの計算シートはマクロを使っていませんのでご安心下さい。
検討の経過
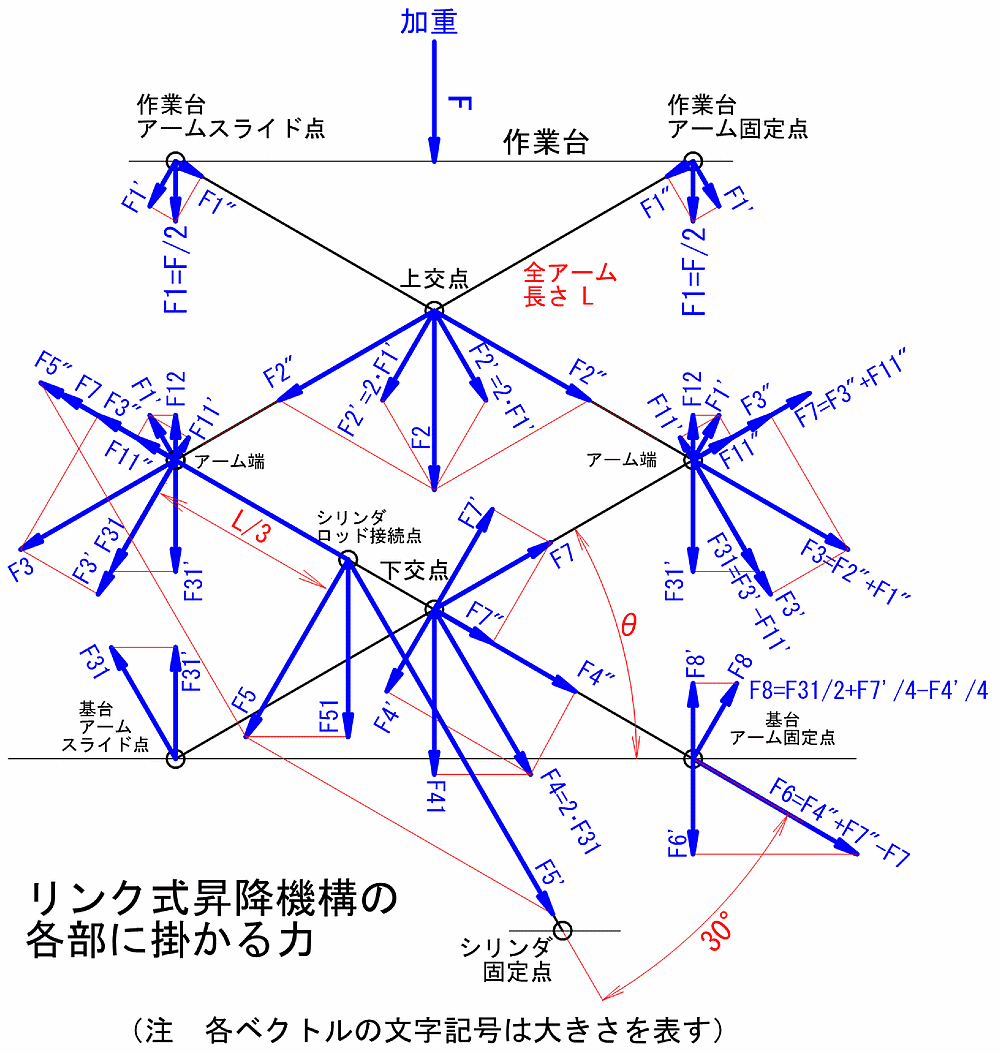
作業台・作業台に載る人と荷物・昇降機構の全ての加重が力として作業台の中央に掛かるものとします。リンク式昇降機構は左右の対であるため片側のリンクには全加重の1/2が掛かります。ここでは片側のリンクに加わる力を F[N] として考えていくことにします。
今回の想定加重は max 200[kgf] 従って F=100[kgf]×9.8=980[N]
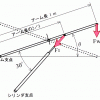
図3は少し上昇してアームの角度が θ となった状態を示しています。なお、計算を簡単にするためにシリンダと押し上げるアームとの成す角は常に30°固定としています。
➀ 作業台はアーム固定点とベアリングによるスライド点で支えられていますが、どちらにも F1=F/2[N]の力が加わるとします。
➁ 「上交点」(上側アームが交わる中央部分)では、それぞれのアームにテコの原理による倍力 F2′ が加わります。この場合の支点は「アーム端」(下側アームとのリンク点)となります。なお、倍力はアームに対して直角方向の成分です。
➂ 左右の「アーム端」には上側のアームを通じて押す力 F3 が掛かります。これにより下側のアームには張力 F7 が生じます。理論上 θ=0[°]のとき F3、F7 は共に無限大となります。(式の中に 1/sinθ の項があると θ=0[°]のときに無限大となる)
実際には構造上 最小θ=3[°] 程度である。このときに F3、F7 は最大となり F3=18700[N]≒1.9[tf] F7=18648[N]≒1.9[tf] 上側アームには大きな圧縮強度が、下側には大きな引張強度が求められる
このように非常に大きな力が掛かります。製作前に心配していたのはこの力で「アーム端」が破断することでした(実際に破断したのは最も下の交点でしたが)。製作前には計算値を出せませんでしたが、ここでやっと出すことができました。
➃ 「下交点」には「上交点」と同様に倍力が加わります。シリンダを無くし基台の「アームスライド点」が固定されていると考えるとわかりやすくなります。そのときの倍力 F4 は「上交点」に掛かる倍力 F2 の約2倍となります。
図3の右上がりアームの下交点に掛かる(静的な)曲げモーメントは、
θ=3[°]のときに最大となり Mb=734[Nm]=74[kgf・m]
理論計算1で予想した Mb は加重がこのアーム側に偏っているとして830[Nm]でした。
➄ 左上がりのアームの「シリンダロッド接続点」に掛かる倍力はちょっと複雑になります。アーム長の2/3の点を支えることから、左上がりのアームから F31×3/2倍 の倍力が、右上がりのアームから「下交点」を経由して (F4′-F7′)×3/4倍 の倍力が掛かり、それらの合成力としてのF5が掛かります。
また、シリンダは常に30[°]の角度で「シリンダロッド接続点」を押すので、シリンダにはその 2倍(1/sin30°)の力 F5′ が掛かります。ただし、シリンダに必要とされる推力の最低は左右のリンク機構分となり F5′ ×2 となります。
実際には θ=3[°]のとき「シリンダロッド接続点」に掛かる倍力の合成は最大となり F5=2930[N]=299[kgf] ・・・ 加重の3倍の倍力が掛かる また、シリンダに必要とされる推力は 2×F5'=11720[N]=1.196[tf]以上 今回のシリンダの推力は最大 2.124[tf] なので約2倍の余裕がある
シリンダに必要とされる推力は、理論計算1で求めた値とピッタリ一致で驚きました。
左上がりアームの「ロッド接続点」に掛かる(静的な)曲げモーメントは θ=3[°]のとき最大となり Ma=489[Nm]=50[kgf・m]
理論計算1で予想した Ma は加重がこのアーム側に偏っているとして653[Nm]でした。
➅ 基台の「アーム固定点」に掛かる力はF6とF8との合成力です。
実際の F6とF8との合成力は θ=45[°]のあたりで最大となり 1845[N]=188[kgf]
「アーム固定点」の軸(パイプ)と軸受けは強度的に強く作ったつもりなので、破損などの心配はないと思っています。
➆ 最下段のアームには部分的に非常に大きな張力が掛かり、理論上 θ=0[°]のときに無限大となる部分があります。
実際には各部の張力は θ=3[°] のとき最大となり 最下段左上がりアームでは 「アーム端」と「ロッド接続点」との間 F7 = 18648[N]≒1.9[tf] 「ロッド接続点」と「下交点」との間 F5"+F7= 23723[N]≒2.4[tf] 「下交点」と「アーム固定点」との間 F5"-F6= 4870[N]=497[kgf] 最下段右上がりアームでは 「アーム端」と「下交点」との間 F7 = 18648[N]≒1.9[tf] 「下交点」と「アームスライド点」との間 0[N]=0[kgf] 各アームには非常に大きな引張強度が要求される。
アーム材そのものの強度だけでなく、交点やリンク点での軸穴や溶接による強度低下が起きるため、その点にも気を付ける必要があります。
⑧ 基台の「アームスライド点」にはスライドレールを持ち上げる方向の力 F31′ が掛かります。
実際のスライドレールを持ち上げる力 F31'は θ=3[°]のとき最大となり F31'=1466[N]=150[kgf]
下のレールやベアリングには強度の高いものを使っていますので、この程度には耐えられると思っています。
まとめ
仮組立て時に起きた破断の原因について、今まで大きな曲げモーメントによるものと考えてきましたが、ここでの計算によりアームの引張強度の不足も大きな原因であったことが分かりました。引張強度不足に加えて(衝撃的な)曲げモーメントが加わったダブルパンチで破断したと考えることができます。
その後行ったアームの徹底補強で今のところ破断は起きていません。アームの曲がりなども今のところは認められません。
スタクセル・エンジニアリング様とのやり取りの中で「構造解析ソフトウェアもありますよ」とご紹介頂きましたが、考えている内に自分の力でもできそうに思えてきたのでチャレンジすることにしました。今回頑張った甲斐があってこのような機構の考え方がわかってきた気がしています。
今回 「数式による理論的な解明」の文章を作成するにあたり「LaTeX」を使いましたが、以前から興味があった「TeX」を勉強する良い機会になりました。
計算は力のベクトル図と三角関数だけで進めましたが行列式を使う方法もあるのかもしれません(「ベクトルと行列」という本がある位ですから)。行列式はよく知らないのですがそちらにもちょっと興味が出てきました。
特に用事の無いときに毎晩計算々々で、1週間以上掛かりましたがやっとの思いで掲載までたどり着きました。年齢的にもちょっときつくて疲れました(農業にも影響が・・・!)。
関連ページ
高所作業車自作 概要
高所作業車自作 その1 主要材料調達
高所作業車自作 その2 理論計算1
高所作業車自作 その3 製作
高所作業車自作 その4 仮組立とアーム破断
高所作業車自作 その5 塗装と最終組立
高所作業車自作 その6 理論計算2
高所作業車自作 その7 強度計算にチャレンジ